Level up and completely transform your mixing with this approach!
“Really?” I hear you ask. Well, look not really, but rather than heading down the road to clickbait oblivion, I offer an alternate approach to perhaps the most important music mixing and production technique, equalisation. (This article assumes you have a basic knowledge of how the equaliser works, so, if you a struggling with that, head on over here for a starter). In any endeavour, be it playing the drums, grinding away at camo challenges in Call of Duty or learning to surf, the road to mastery is long and unforgiving. Writer Malcolm Gladwell popularised the idea that 10 thousand hours of concerted effort will yield greatness in any given field, regardless of natural talent. Hopefully, the Harmonic Equalisation approach, combined with a few hours of tweaking and experimentation can help you further down the road to your 10 thousand hours.
Let’s head down a rabbit hole and look into the maths and physics of music.
Read all the latest features, columns and more here.
First let’s look at the word: Harmonics. The image below shows the spectrum analyser of a sine wave at 100Hz. On its own, I’m sure you’ll agree, the sound is quite dull and lacks character (listen). That said, it’s still useful in many genres and hip hop, without a sine wave 808-style kick, would simply not be hip hop but nonetheless, it sounds very plain.
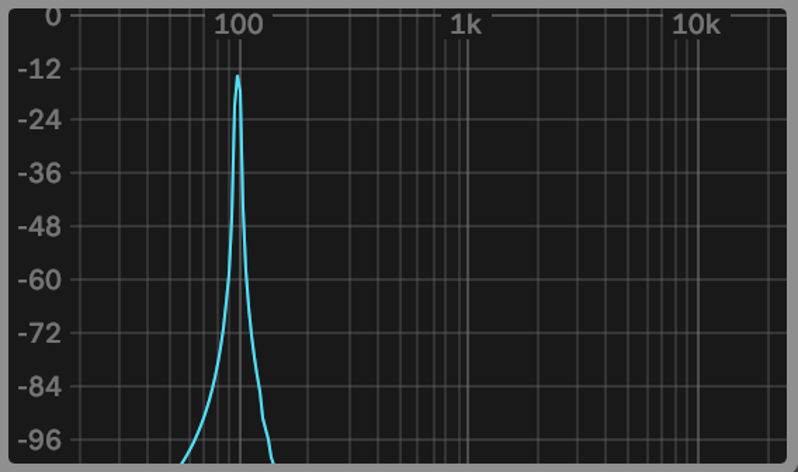
The pure sine wave above, devoid of harmonics, is simple to generate on a synthesiser. However, it is impossible to generate a such a sine wave on an acoustic instrument. When a note is played on an acoustic instrument, we hear the actual note being played, known as the fundamental, and a series of harmonics, or overtones above the original note/frequency at varying volumes.
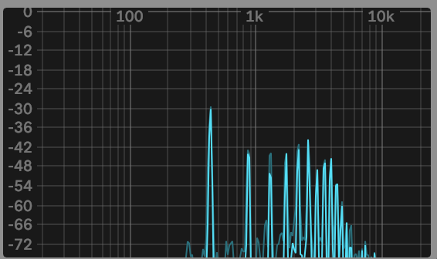
These harmonics occur in what is called the Harmonic Series. Depending on the instrument, each different harmonic is heard at various levels. This phenomenon is what gives each instrument its unique sound. Have a look at the images below to see the same note, in this case a concert A or A4 depending on your preference, with a fundamental of 440Hz, played on a variety of instruments.
Violin
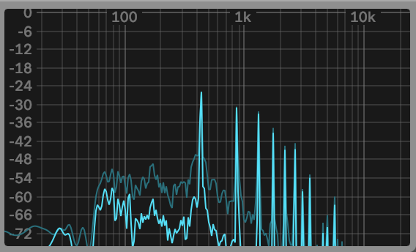
Piano (n.b. the frequencies seen below 440Hz are the sound of the piano hammer striking the strings, not the fundamental note of 440Hz)
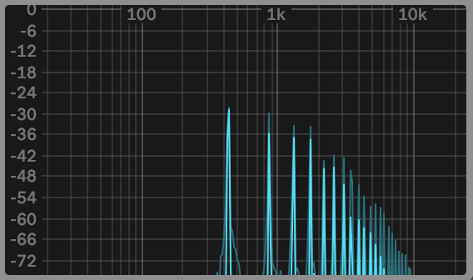
Trumpet
Clean Electric Guitar (n.b. The frequencies seen below 440Hz are from the plectrum, striking the strings).

Overdriven Electric Guitar (n.b. There are noticeably more harmonics and these are higher in gain due to the overdrive).
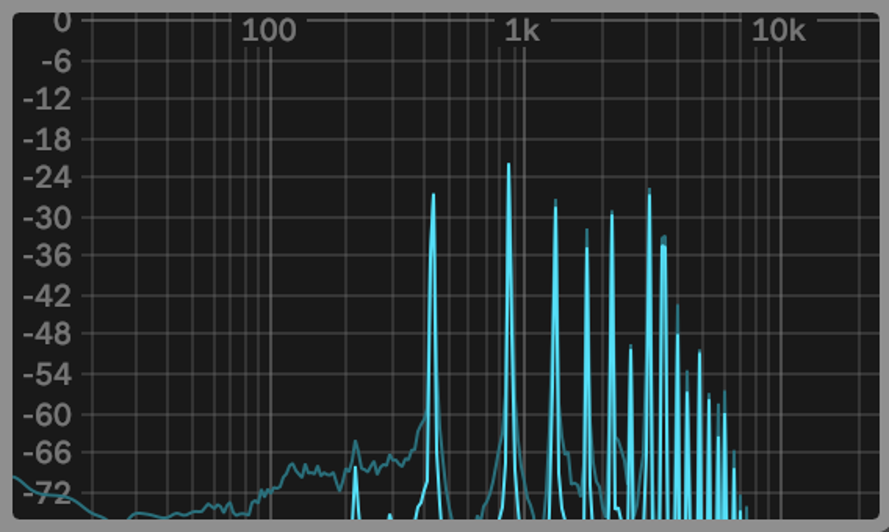
When looking at these images, we can clearly see the different height and number of the harmonics. This phenomenon is what gives each instruments its own unique sound, and no two instruments will have the same harmonics. Often, more expensive instruments are made from rarer materials that are more resonant, which in turn, produces a sound, richer in harmonic content which listeners find subjectively more pleasing. The most fascinating aspects of the harmonic sequence is the actual frequencies heard above the note’s fundamental frequency.
These all have a musical and mathematical relationship to the fundamental. This sequence remains constant for all instruments, only the volume of each harmonic changes. The image below shows the harmonic sequence above an A4 440Hz fundamental, with all harmonics shown at the same volume.
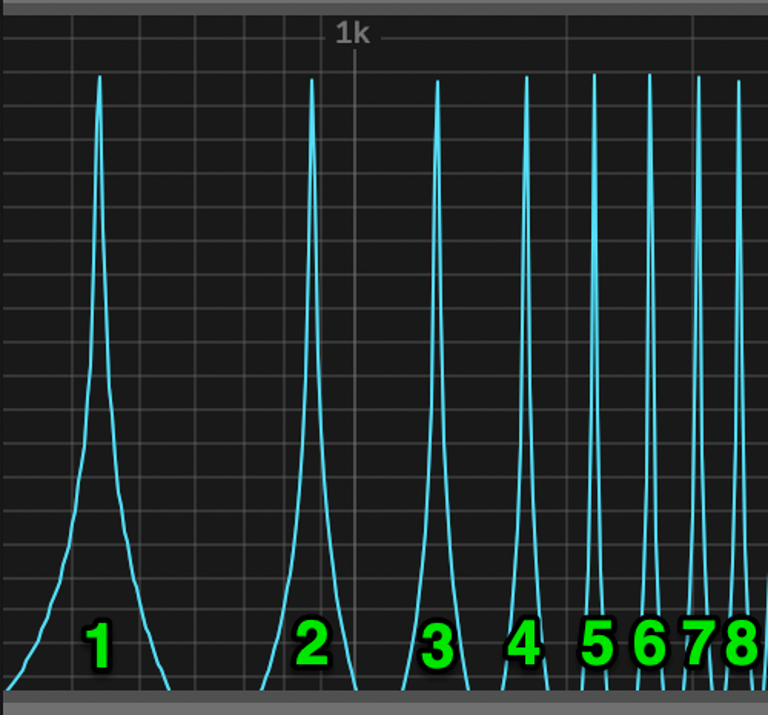
The interval between each harmonic can be expressed as notes, frequencies and ratios as follows:
1st Harmonic – A4 or 440Hz: The fundamental, or, the note that is being played;
2nd Harmonic – A5 or 880Hz. two times the frequency of the fundamental: One octave above the fundamental:
3rd Harmonic – E5 or 1320Hz, three times the frequency of the fundamental: One octave and a fifth above the fundamental;
4th Harmonic – A6 or 1760Hz, four times the frequency of the fundamental: Two octaves above the fundamental;
5th Harmonic – C#6 or 2200Hz, five times the frequency of the fundamental: Two octaves and a third above the fundamental;
6th Harmonic – E6 or 2640Hz, six times the frequency of the fundamental: Two octaves and a fifth above the fundamental;
7th Harmonic – G6 or 3080Hz, seven times the frequency of the fundamental: The octaves and a flattened seventh above the fundamental;
8th Harmonic – A7 or 3960Hz, eight times the frequency of the fundamental: Three octaves above tthe fundamental.
So, how can we use this information to approach EQ decisions? As we have seen above, the sound of any given instrument or synth comes from a unique combination of the fundamental note and the resulting harmonics. When we look at these spectrum charts, we see that the fundamental of 440Hz is the most prominent in each of the sounds, and the harmonics vary in volume considerably. When more than one instrument is mixed together, however, this fundamental frequency will sum and become even louder. The fundamental becomes overpowering, yielding a muddy sound that makes it difficult to hear individual instruments. This can be countered by reducing some of the fundamental with an EQ cut at this 440Hz.
Doing so will reduce this common frequency of 440Hz and accentuate the harmonics, the part of the sound that makes a piano sound like a piano, a violin like a violin etc. Put simply, it reduces the muddiness and increases the most exciting parts of the sounds. Be careful though. If you reduce the fundament too much, the instrument will sound hollow. However, the right amount of reduction, in the context of a full mix, will stop the frequency build up at the fundamental and provide greater clarity.
To illustrate the point, let’s look at some notes and corresponding fundamental frequencies for some guitar chords and bass notes. Assume the song is built around four chords. The Axis of Awesome four chords will do nicely. The progression and frequencies can be summarised as follows:
| Chord | Guitar Frequency | Bass Frequency |
| G Major | 98Hz | 49Hz |
| D Major | 146.8Hz | 73.4Hz |
| E Minor | 82.4Hz | 41.2Hz |
| C Major | 130.8Hz | 65.4Hz |
It’s surprising how low the bottom E of the bass guitar is, I know! Few audio headphones and speakers will reproduce that frequency so most of what we hear in the bass guitar, is actually the harmonics. Our ears trick us into hearing the 42.1Hz, a phenomenon sometimes referred to as a missing fundamental. Our ears hear the harmonics above the fundamental and our brain fills in the missing lower frequency.
In this example, the entire guitar chord progression spans less than an octave, running from 82.4Hz to 130.8Hz. So, if we reduce some of the bass frequencies in the guitar with a parametric EQ around 120Hz with a bandwidth of one octave (Q factor of 1.41), we affect frequencies from approximately 75Hz to 150Hz. All of the guitar fundamentals in the progression will be reduced, making the upper guitar harmonics clearer and more interesting as a result.
This reduction in the guitar’s low frequency fundamental, will make the second and third harmonics in the bass guitar more audible, and the bass guitar will appear louder. This in itself is not surprising but knowing the frequencies of the chords being played will allow us to make more informed decisions about frequencies to cut or boost. Instead of setting a parametric band to a 20dB boost and sweeping it around until you find the “magic” frequency, dial in a 3dB to 6dB cut based on the music being played and switch the bypass on and off, to hear if the EQ is helping or not.
As a mix engineer starting out, there’s nothing more frustrating than hearing someone say “I just EQ until it sounds good.” Using the Harmonic Equalisation approach, we have a starting point. The approach can be applied to the mid and high frequencies too. An octave is simply a doubling of frequencies, so it is easy to go looking for frequencies in the mids and highs, based on this. To accentuate the G chord, go looking at 382Hz for warmth. For loudness, keep on doubling those frequencies. Start at 764Hz or 1528Hz. Brilliance can be found at 3kHz or 6kHz and on it goes. If mental arithmetic is not your forte, fret not.
There are many EQ plugins out there that feature piano keyboards the show the corresponding note for each frequency such a FabFilter’s legendary Pro Q or Waves H-EQ. That Ableton EQ Eight provides the same information when you hover the mouse above the interface, as well. Izotope’s Nectar vocal processing plugin has an EQ that moves the frequency band around to chase the fundamental depending on the note being sung. Impressive! Of course, compression, saturation, and distortion create huge amounts of harmonics, so experiment with these processors instead of an EQ.
As always, avoid using the solo button at all costs! Who cares what the instrument sounds like in isolation. No one will hear that! Now, go, log some of those hours 10 thousand hours. Happy tweaking.
Get into the science of harmonics here, with our friends at Yamaha.







